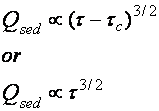Slope length modified diffusion; A demonstration that sheetwash type processes lead to diffusion like processes with a slope length dependant diffusion coefficient.

Demonstration that Q_{sed per width} ~ C x tan a

Assume a uniform rainfall rate ( R) and a uniform infiltration rate (I). Also assume uniform soil characteristics. We will also assume that any sheetwash water flow behaves according to the Chezy equation, and that sediment transport can be approximated by the Meyer-Peter-Muller equation. These assumptions are all reasonable, but it unlikely that they could hold in any real world situation, which has pervasive heterogeneity. Nevertheless, this development shows that a simple modification to simple diffusion can be made for slope length dependant distributed processes, and that such a modification may be reasonable.

In the following, x is the distance downslope from the interfluve, a is the slope angle, S is the slope (tan a), t is the basal shear stress created by the sheetwash, and most coefficients get dropped out of equations since we are only interested in the proportional relationships. Upper case Q has been used to indicate flux per unit width.

(a) Assume Chezy equation gives average water velocity		Note: slope is a constant at any location so that only h, the water depth, and v, the velocity, can vary. (see note below on Manning equation)
(b) Assume MPM equation gives a scale for soil transport		Note: we make the argument that tc is effectively zero, because soil particles are constantly being dislodged by rain impacts, not by excess basal shear stress. Also the MPM coefficient A has been eliminated by the proportional sign.
(c) Shear stress		As always
(d) The accumulation of water downslope under uniform rainfall
(e) Note that (a) times the depth of flow gives an alternate equation to (d) for water discharge.		Noting that water discharge per width is defined as , where v is the average velocity.
(f) Also note that using (c) in (b) gives an expression for sediment transport in terms of flow depth and slope		Dropping rg
Then we note that (f) can be written in terms of water flow (e)
Finally, we note that water discharge is also given by (d), which gives:
Which gives the finally result that sediment transport under sheetwash (with all the simplifying assumptions) goes as:		Where the C is added to convert the proportionality to a relationship
This demonstrates that using a modified diffusion approach for sheetwash is reasonable.		Note, this approach glosses over many of the problems. The biggest problem is the generation of Rills and Gullies which do not follow the outline above, and which show that our result must be used with caution.

Notes:

The Manning equation is probably the most used bulk flow relationship for determining flow velocity or discharge in natural water flows. It’s accuracy depends heavily on the choice of the roughness parameter n (see http://wwwrcamnl.wr.usgs.gov/fieldmethods/indirects/nvalues/index.htm ). We have used the less common Chezy equation here. Our main reason is (quite honestly) because it gives a slightly simpler result. The choice between the 2 equations is very minor since they vary only by depth to the 1/6 power. The Manning equation is much more common in North America.

The Meyer-Peter-Muller is one of the simplest and most frequently used total load equations for sediment transport in fluvial settings. It is not very good, because it only captures the barest physics of the transport problem. Despite its failings, it is usually one of the best general indicators of sediment transport out there. Probably its main attribute is that: although rarely correct, it is unlikely to be very wrong. The characterization of tc and A are problematic and although empirical methods exist, they are usually best determined by back-calculation.