Homework #10 2018, Earth Surface Processes, Humphrey

The 4^th question looks complex, but is just solving a cubic equation. Don’t panic, there are cubic equation solver apps out there in web-land. There are a lot of calculations in this homework, take your time and think a little.

1 a. In class we did a rough estimate of the hydraulic radius (the R in the Mannings eqn.). Let’s do a better job: estimate the Hydraulic Radius of the Laramie River at minor flood, 1m deep and 4m wide. Assume a trapezoidal channel shape, 4m wide at the surface, with straight 45 degree sloping banks, so that the ‘thalwg’ or middle (flat) section is 2m wide

b. Search the web for an appropriate value of Mannings ‘n’ for the Laramie river. You will have to look at pictures of other rivers and find one that looks similar. The USGS has a good web site for this. Calculate the Manning velocity and discharge of the Laramie river in minor flood. Use a depth of 1m and a slope of 5x10^-4.

2. We have talked about the variability of river discharge. There are many ways of looking at how river discharge varies. A useful type of plot is shown below, which nicely shows that the Laramie river typically has only one flood (snow melt dominated) in early summer.

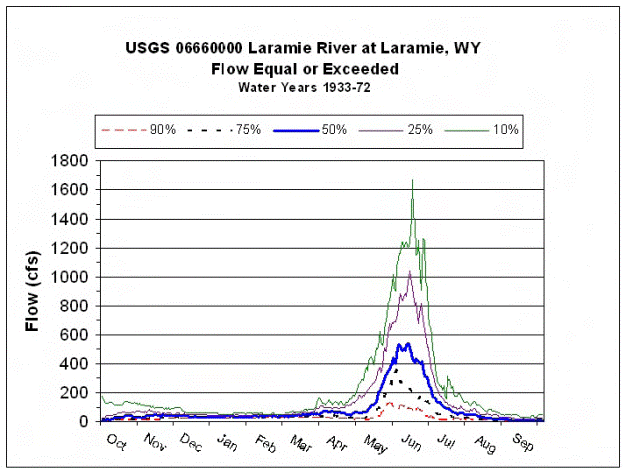
For this exercise, we are going to look at something that is of major interest to many, the question of the likelihood of large floods. Here is some data from the Laramie river at Laramie:

Flow measurements as reported on UPRR quarterly Discharge Monitoring Reports (DMR) for WDEQ Permit WY0032590,

Laramie Tie Plant.

Year

Oct Nov Dec Jan Feb March Apr May June July Aug Sept

Streamflow (cfs)

1987 8.1 77 49 54 65 62 157 46 22 7.8 4.5

1988 28 40 26 7.9 7.0 68 201 508 680 48 8.9 5.5

1989 17 44 34 7.1 2.0 61 nr 16 45 13 11 13

1990 36 75 60 27 30 189 36 30 351 50 20 10

1991 7.9 41 76 11 24 104 20 169 612 19 21 11

1992 231

1993 49 102 147 196 264 309 39 407 1016 115 11 36

1994 14 38 67 177 209 93 53 288 77 7.6 7.0 4.7

1995 45 55 53 86 65 68 6.8 111 1281 281 14 15

1996 51 62 88 77 68 79 107 552 1136 420 20 21

1997 115 128 115 55 62 82 101 503 1277 149 110 87

1998 34 55 63 70 75 87 100 305 425 139 66 29

1999 20 18 67 56 60 75 68 496 1126 267 20 17

2000 18 40 13 84 72 45 54 297 101 18 6 13

2001 56 20 54 77 90 75 21 177 66 11 18 26

2002 11 16 21 160 207 174 32 68 56

2003 18 49 68 28 22 22 20 230 556 14

2004 131 122 113 68 83 72

2005 47 49 81 94 98 90 53 306 1115 95 80 16

2006 188 201 200 126 109 107 159 386 105 187 109 115

2007 143 104 68 200 186 281 146 549 378 78 109 34

2008 68 68 68 98 469 1715 316 180 169

The above table shows typical problems with flood analysis. Real data sets have missing and questionable data. The above table lists measurements taken once a month, obviously it probably misses the actual flood peaks. There are more subtle problems with stream data: even if you find more continuous data (e.g. USGS typically reports daily discharge), the actual discharge is not measured, but estimated from river depth. Any bed or bank erosion or deposition will create errors in this depth based estimate, this is especially a problem at high flows when erosion/deposition is common. The biggest problem with the Laramie river data, is that over time, various water projects have diverted water from the river. As a result, the flood data is not ‘stationary’, in other words the flood data does not represent a sample from the same river over time. The river has been changing, so that we can’t trust the old data to predict the future.

Question 2.

Use Google Earth to find the width of the Laramie river near Optimist Park, specifically near the bridge on W Garfield st..

a) The largest flood in the above record was in 2008, at 1715cfs. How deep would this flow have been under the Garfield bridge, IF the river stayed in its banks. Use Manning’s equation, and the slope from previous question. [hint remember discharge is w*v*d, and you will have to convert from cfs to m^3/s]

b) Hard, if you had to use the data in the table for a specific purpose, such as calculating yearly discharge: 1- how would you use the data for April 1995? 2- And how would you deal with the data for 2002 thru 2004. 3- Is there anything you can do with the 1992 data?

Question 3, recurrence intervals or ‘100 year floods’

Grey River, at Dobson New Zealand

1968 to 2004

year	Max flow (m3/s)
1997	5950.8
1988	5840.4
1998	5670.0
1970	4899.1
1994	4844.5
1977	4841.4
1984	4814.3
1983	4228.2
1969	4203.4
1972	4125.6
1975	4117.8
1980	4039.4
1973	4012.5
1979	4000.9
1982	3975.2
1996	3866.7
2000	3809.5
1974	3771.7
1968	3678.3
2002	3517.9
1976	3463.4
1981	3448.9
1993	3422.3
2001	3342.7
1978	3302.9
2004	3224.6
2003	3221.9
1989	3217.1
1995	3185.8
1992	3177.6
1991	3091.4
1999	3070.0
1990	2806.8
1971	2420.5
1987	2385.4
1986	2364.9
1985	1794.8
	Mean 3761.0

Question 3

To continue thinking about river floods, we will look at some better quality data from the Grey river.

a. Calculate the recurrence intervals for floods on the Grey River. Recurrence intervals are what are usually somewhat misleadingly quoted in the popular media as the 100 year flood or whatever the news person wants to emphasize. There are a variety of methods to calculate recurrence interval, but probably the simplest is as follows: order your data from largest to smallest (this I have done for you). Now apply the following formula to each datum:

T_r = (N+1)/n, where N is the total number of observations, n is the ranking in the above list from top to bottom (eq the second from the top is n=2) and T_r is the recurrence interval in years.

b. Plot the recurrence intervals on a semi log plot. Use log time on the x-axis and discharge on the y-axis. We will use a log axis, however there is considerable discussion in the literature about the expected shape of a recurrence interval curve, or more precisely, how floods should be distributed in time. (If you would like to investigate this more, look up Gumbel Distribution on the web.) We use a log plot since it is straightforward to plot, not because it is correct.

c. Use your plot to estimate the 100year flood on the Grey river. Comment on the accuracy of your prediction.

d. The channel forming discharge for a meandering river is typically about the 2year flood. What is the 2 year flood on the Grey River.

4 (this weeks geomorphic puzzle) In class I quickly sketched the energy argument for the difference in behavior of super-critical and sub-critical flow. The development in class was a sketch of the tradeoff between potential energy and kinetic energy. I want you to understand this important concept: that water only has so much energy, and the trade off from kinetic to potential (or vice versa) controls a lot of the rivers behavior. I would like you to follow the logic outlined here and find solutions to illustrate this behavior.

Consider a rectangular channel of constant width and steady discharge, which has a small bump of height ‘h’ which the flow must cross. Assume the slope of the flow is so low that we can ignore it and set the elevation of the bed of the incoming flow to be 0, while the bed of the flow over the bump is just h. We will call the initial location 1 and the location at the bump 2.

The incoming depth is d₁ and the incoming velocity is v₁, since the width is constant, we just look at a 1m wide section of this flow. The flow over the bump will have depth d₂ and velocity v₂, and the water surface height over the bump is d₂ + h. Although we don’t yet know values for d₂ or v₂: they will tell us if the water surface goes up or down, and that is what we solve will for. The mass flux of water per time incoming is r*v₁*d₁ and the mass over the bump is the same (or equivalently r*v₂*d₂).

The kinetic energy of the water is the mass times the square of the velocity divided by 2, while the potential energy is the mass times gravity times the height (d₁/2). To get the total energy in a column we must multiply by the depth. Since the flow velocity is changing, it is important to multiply by the local velocity (v), to get a total energy flux per unit width per time at each of the two locations. We assume no energy is lost between points 1 and 2, and so we can write the energy balance for K.E. and P.E. as a statement that the energy flux per time at the two places is equal: [equation A]:

r*v₁³*d₁/2 + r*g*v₁*d₁ *d₁/2 = r*v₂³*d₂/2 + r*g*v₂*d₂ *(d₂/2 + h) ,

where we have been careful to include the extra height of the bump (h) in the potential energy at location 2. This simplifies considerably since r*v₁*d₁ is equal to r*v₂*d₂ . Further simplification occurs if we write v₂ = v₁*d₁/d₂ and multiply the whole equation by d₂², to get [equation B]:

0 = [g*v₁*d₁] *d₂³ + [2*g*d₁*v₁*h - v₁³*d₁ - g*v₁*d₁²] *d₂² + [v₁³*d₁³ ],

where all terms in ‘[ ]’ brackets are known if we know v₁*d₁ . This is a cubic equation in d₂ . (e.g. the equation is simply 0 = a*d³ + b*d² + 0*d + c)

a. Write equation A and write what each term represents, and produce equation B by the indicated steps.

b. To see what the Laramie river might do in encountering a bump in the bed, try putting an input velocity of 1m/s, a depth of 1m, and a bump height of 0.1m. How much does the water surface drop over the bump? (don’t forget to add the height of the bump to get the water surface. You can directly solve the cubic, or use a web app. [you are looking for the real root] Or it is a fairly quick iteration to get a solution: try a d₂ of 0.6m to start, improve on that if you can)

c. If you have made it this far; Finally, just to see the opposite behavior for high F_r number flow, try this with a (unrealistic) flow velocity of 5m/s, depth of .5m and bump of 0.1m.